13 Maio

Belém

Aprenda que fazer a quadratura do círculo é impossível com régua e compasso

Quadrar um círculo significa encontrar um quadrado cuja a área seja igual a área desse círculo. Muito fácil, não é?
Basta usar equações da geometria plana e igualar a área do quadrado com a área desse círculo

 

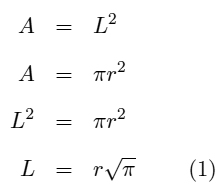
Mas não é tão simples assim. Esse é um problema grego, do tempo de Euclides, e é para ser resolvido com uma construção geométrica usando apenas compasso e régua. Uma régua que não seja milimetrada. Na grécia chegava-se a dizer que o círculo não tinha área porque não tinha quadratura.
Professores de desenho gemétrico, nas universidades, ensinam uma solução simples e que pode ser feita com régua e compasso. No quadrado ABCD, da figura abaixo, marca-se o ponto médio E de CE e traça-se a reta AE de comprimento x.

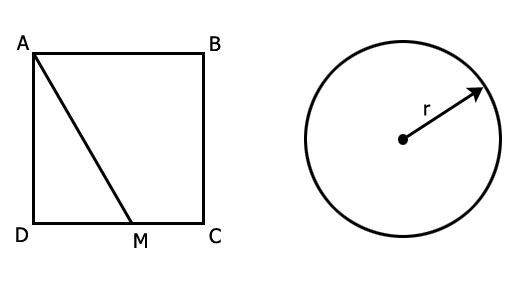
O raio do círculo é igual a metade x, ou seja r/2, então x = 2r. Para calcular x, usamos o teorema de Pigágoras:

Comparando a equação (2) com a equação (1) vemos que existe uma aproximação 3,2 para pi, ou seja, esse resultado não é exato. Na verdade esse problema não tem solução para construção com régua e compasso e 2 mil anos depois de lançado, Gauss é quem mostra que não existe tal solução.